Computation Systems of the Middle Ages
Welcome to Cosmographia — a newsletter dedicated to exploring the world. This post is part of our Manūscriptum series, where we take a look back at some history’s most beautiful documents. For the full map of posts, see here.
Histories of computing tend to either begin with ancient efforts — like the abacus, Archimedes’ mechanical theorems, and Aristotle’s logic — or they skip ahead to the early modern period, recounting stories of Gottfried Leibniz’s calculating machine, Charles Babbage’s Difference Engine, or Ada Lovelace’s recursive algorithm. That is, if they haven’t jumped straight ahead to the work of the Claude Shannons, Konrad Zuses, and Alan Turings of the 20th century.
Rather neglected in this story are the parts in between: the weird and wonderful contributions of the Middle Ages. As I’ve written elsewhere, the Dark Ages weren’t all that dark, and this period of intellectual history is rather hard done by. To remedy this shortcoming, here are four computation systems from the Middle Ages you have (probably) never heard of.
I. Logic Trees of Breviculum
Ramon Llull (c. 1232-1316) was a theologian, poet, and knight from the Kingdom of Majorca. He was also — though he didn’t know it — something of a proto-computation theorist. Among his many achievements was the invention of a logical theory of knowledge, published in his Ars Magna, a text which set out a model designed to prove the truth of the Christian doctrine, and thus convert non-believers.
Llull’s system of universal logic began with a set of general principles (axioms) based on the sixteen Dignities (e.g. Goodness, Wisdom, Glory etc.). Each principle is assigned a letter, like in algebra — e.g. “B: Goodness is that whereby good does good” — and then these are combined with other principles through a series of iterative operations — systematised by his rotating disc devices called ‘Lullian Circles’ — to produce knowledge. His work, which Leibniz later termed ars combinatoria, can be seen as a very early attempt to mechanise reasoning.


Unusually for his time, Llull used letters and diagrams in his system, giving the work an algorithmic quality. Some have thus argued Llull’s system is the beginning of information science. It is perhaps best illustrated in his student Thomas Le Myésier’s work, Breviculum (c. 1321), who drew the model as a series of logic trees:



II. Mediaeval Numerals
Hindu-Arabic numerals are now ubiquitous across the world, but before they became universal, there were others.
You have likely already heard of Roman numerals, but there was another European numerical system used in the Middle Ages, one invented by an order of French monks in the 13th century. Each numeral in the Cistercian system is built around a vertical line, which acts as an axis of four quadrants. The upper right quadrant symbolises the units, the upper left the tens, the lower right the hundreds, and the lower left the thousands. The different variations of lines that appear in each quadrant symbolise the value of each place, which together form the number.
While this simplifies large numbers into a single glyph, the system is hindered by the fact that it makes it very difficult to do harder operations — like long division or subtraction calculations.
During the same period, Chinese merchants, mathematicians, and astronomers were using a counting rod numeral system. This grew out of an oracle bone script that developed during 14th-century BC Shang Dynasty.
Meanwhile, over in the Americas, the Maya developed a vigesimal (or base-20) numeral system, not unlike the Yoruba’s in West Africa. The Maya use a series of dots and dashes to form their numbers.

III. Consanguinity Tables
In 506 AD, functionaries for Alaric II, King of Visigoths, published the Lex Romana Visigothorum — a collection of laws and legal writings that were used in southwestern Europe throughout the Middle Ages. Among the various legal frameworks discussed therein was a section on inheritance law, which was an important business for those with titles, wealth, and hereditary privileges.
In the below manuscript copy from the 9th century, the scribe has drawn geometric panels for determining degree of kinship. The reader is indicated in the centre as ‘Ego’; those above are ancestors; those below are descendants; to the left and right are siblings and cousins of varying distance.
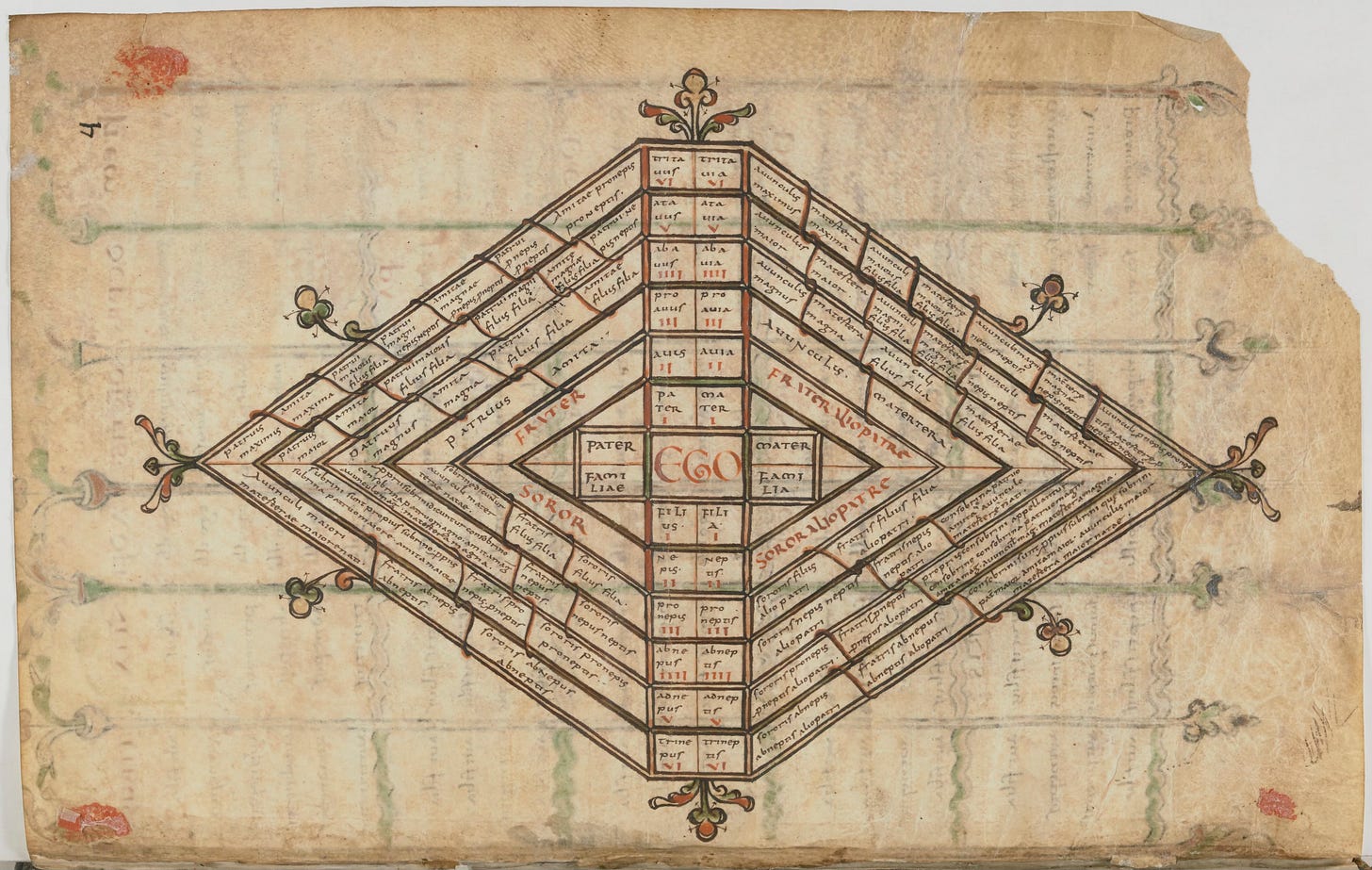
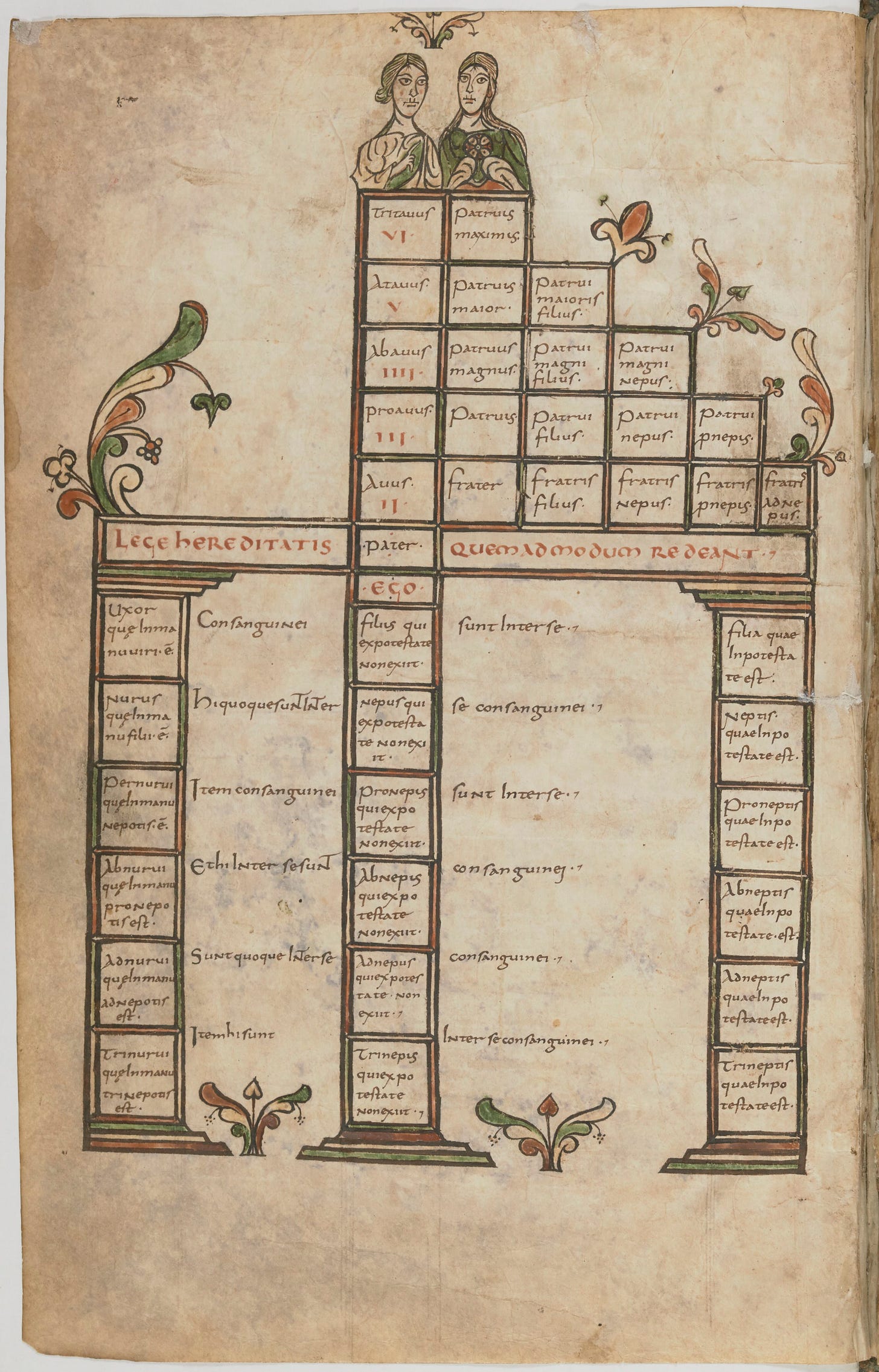
Another important time to map familial relationships was in the case of marriage. The Middle Ages saw the Roman Catholic Church tighten up rules around marrying close relatives, and thus consanguinity tables become common in theological manuscripts, like this one from a 12th-century edition of Isidore of Seville’s Etymologiae:
In the centre are the parents of the candidates for marriage, their forebears are above, siblings and their progeny are either side, and direct descendants are below. In the Middle Ages it was very important to use one of these tables so you didn’t accidentally marry your sister!
IV. Computing Orbits
Scientific manuscripts from the Middle Ages tended to be littered with computistical writing on astrology, calendar calculations, and astronomical observations, including descriptions of the epicycles of the planets, the Moon, and the Sun (then thought to orbit the Earth). These texts often attempted to reconcile Ptolemaic cosmography with Christian theology, an endeavour that required quite sophisticated, albeit flawed, mathematics.
For example, below are two of the earliest uses of a line graph in the study of physics:


One of the central tenets of Mediaeval scholarship was the ability to calculate astronomical calendars. A popular method of learning this complex technique was a mnemonic device sometimes called computus manualis (manual calculation), where monks would inscribe dates on their joints as a calculation aid. The below diagram illustrates how this was done.
Perhaps the most beautiful of all the cosmographical texts of the Middle Ages is that found in the first two leaves of the Catalan Atlas. Containing charts for calculating days, tides, holiday dates, and even a little sketch of the human anatomy, these leaves were less for practical use than they a presentation of an ordered cosmos for the King of Aragon, who (probably) commissioned the work.
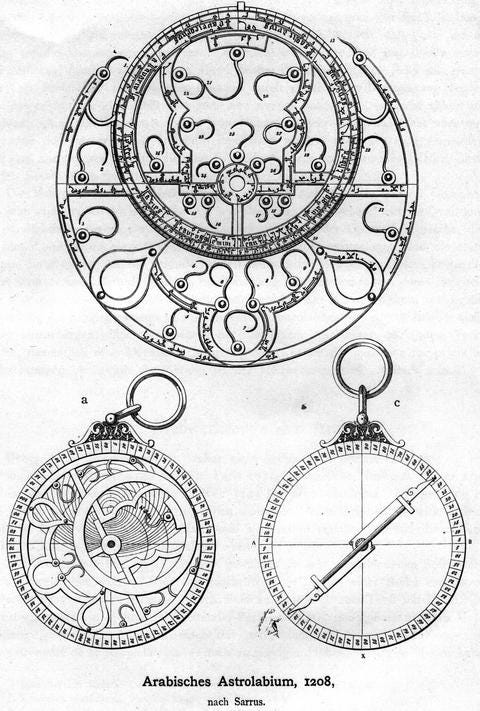
Finally, we cannot end our discussion of astronomical computation without mentioning perhaps the most sophisticated calculation instrument invented during the Middle Ages: the astrolabe.
While it’s possible ancient scholars like Hipparchus and Hypatia may have constructed a rudimentary version of the instrument, it was not until the early Middle Ages that the astrolabe was perfected. In Baghdad’s House of Wisdom, the 8th-century mathematician Muhammad al-Fazari built the handheld device that could tell you the time, your location, correct orientation, and, perhaps most importantly of all, your horoscope.













Fantastic! Not to mention, a thousand years earlier, Archimedes or someone like him had designed (and had built) a working analog computer, the Antikythera mechanism. I frequently think about how differently things might have gone, had that knowledge spread instead of being buried. Same w/Lovelace/Babbage during the Victorian era.
I am a total proto-science nerd. All this stuff is just fascinating, isn't it? Those early charting efforts make it so clear- human beings seek clarity and understanding in all we do. The con-sanguinity tables are touching in their earnestness. When young boys were farmed out to relatives and allies as proto-hostages to grown up with broader loyalties, understanding who you might be related to by blood was a real concern. Another great read! And those first pages of the Catalan Atlas are stunningly beautiful.